Ancestors Datalog Example (short trace version)

The classic example to showcase Logic Programming, running on Takmela/Datalog! This example has a relatively straighforward query with a short trace.

All ancestors examples: Short / Medium / Longer trace. (Note that the fact set is slightly different in each example)

parent("a", "b").
parent("a", "c").
parent("b", "d").
parent("d", "e").

ancestor(X, Y):- parent(X, Y).

ancestor(X, Y):- ancestor(X, Z), ancestor(Z, Y).

ancestor(b, X)

In the actual trace we use 'a' to mean ancestor and 'p' to mean parent.

Hint: Hovering over a graph expands it

Trace appears confusing? This might help

Call start rule
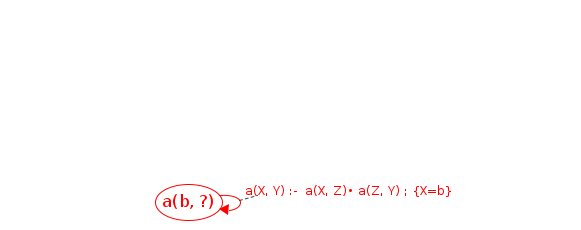	#0: Called a(b, ?) at the top level (will process) Processing a(b, ?) codePos a(X, Y)→•p(X|b,Y) Calling fact: p(b, ?) Found fact: p(b, ?) → [b, d] Processing a(b, ?) codePos a(X, Y)→•a(X|b,Z), a(Z,Y) Calling: a(b, ?) [already processed]
p(b, ?) → [b, d]
Iteration 0
Worklist - successes jS p(b, ?) → (b, d) Worklist - continuations nJ a(b, ?) → a(X, Y)→a(X|b,Z)•a(Z,Y) S⤚ p(b, ?) → a(X, Y)→p(X|b,Y)•
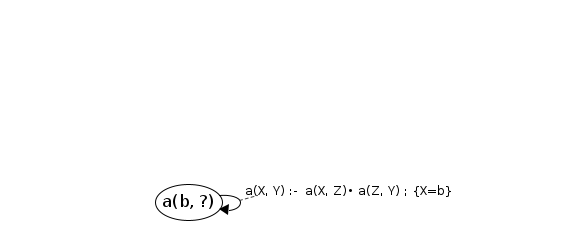	#1: JoinS: p(b, ?) → [b, d] will resume cont: a(X, Y)→p(X|b,Y)• newVars: {Y=d} Processing a(b, ?) codePos a(X, Y)→p(X|b,Y|d)• Reached end of rule, success! a(b, ?) → [b, d]
p(b, ?) → [b, d] a(b, ?) → [b, d]
Iteration 1
Worklist - successes jS a(b, ?) → (b, d) Worklist - continuations
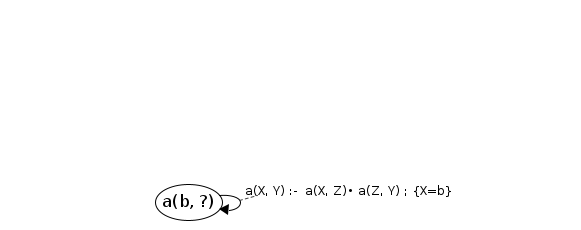	#2: JoinS: a(b, ?) → [b, d] will resume cont: Root("b", V0)→a("b",V0)• newVars: {V0=d} Processing Root() codePos Root("b", V0)→a("b",V0|d)• Reached end of rule, success! Root() → [b, d]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓
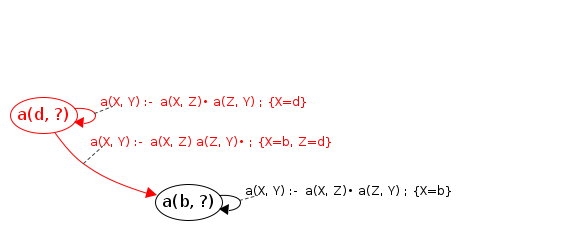	#3: JoinS: a(b, ?) → [b, d] will resume cont: a(X, Y)→a(X|b,Z)•a(Z,Y) newVars: {Z=d} Processing a(b, ?) codePos a(X, Y)→a(X|b,Z|d)•a(Z|d,Y) Calling: a(d, ?) [will process] Processing a(d, ?) codePos a(X, Y)→•p(X|d,Y) Calling fact: p(d, ?) Found fact: p(d, ?) → [d, e] Processing a(d, ?) codePos a(X, Y)→•a(X|d,Z), a(Z,Y) Calling: a(d, ?) [already processed]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e]
Iteration 2
Worklist - successes nJ Root() → (b, d) jS p(d, ?) → (d, e) Worklist - continuations nJ a(d, ?) → a(X, Y)→a(X|d,Z)•a(Z,Y) nJ a(d, ?) → a(X, Y)→a(X|b,Z|d), a(Z|d,Y)• S⤚ p(d, ?) → a(X, Y)→p(X|d,Y)•
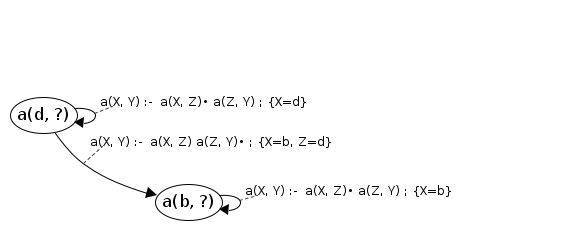	#4: JoinS: p(d, ?) → [d, e] will resume cont: a(X, Y)→p(X|d,Y)• newVars: {Y=e} Processing a(d, ?) codePos a(X, Y)→p(X|d,Y|e)• Reached end of rule, success! a(d, ?) → [d, e]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e] a(d, ?) → [d, e]
Iteration 3
Worklist - successes jS a(d, ?) → (d, e) Worklist - continuations
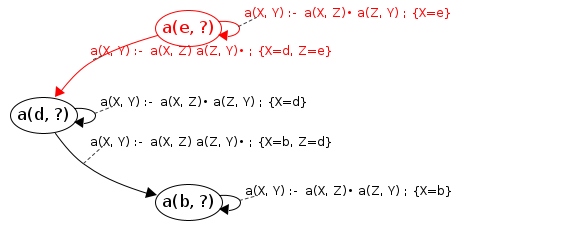	#5: JoinS: a(d, ?) → [d, e] will resume cont: a(X, Y)→a(X|d,Z)•a(Z,Y) newVars: {Z=e} Processing a(d, ?) codePos a(X, Y)→a(X|d,Z|e)•a(Z|e,Y) Calling: a(e, ?) [will process] Processing a(e, ?) codePos a(X, Y)→•p(X|e,Y) Calling fact: p(e, ?) Processing a(e, ?) codePos a(X, Y)→•a(X|e,Z), a(Z,Y) Calling: a(e, ?) [already processed]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e] a(d, ?) → [d, e]
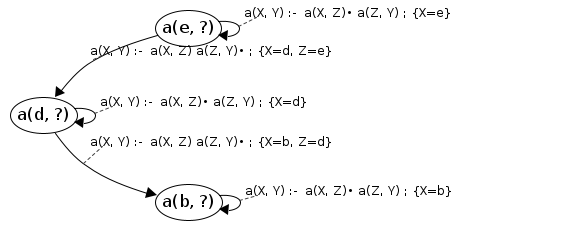	#6: JoinS: a(d, ?) → [d, e] will resume cont: a(X, Y)→a(X|b,Z|d), a(Z|d,Y)• newVars: {Y=e} Processing a(b, ?) codePos a(X, Y)→a(X|b,Z|d), a(Z|d,Y|e)• Reached end of rule, success! a(b, ?) → [b, e]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e] a(d, ?) → [d, e] a(b, ?) → [b, e]
Iteration 4
Worklist - successes jS a(b, ?) → (b, e) Worklist - continuations nJ p(e, ?) → a(X, Y)→p(X|e,Y)• nJ a(e, ?) → a(X, Y)→a(X|d,Z|e), a(Z|e,Y)• nJ a(e, ?) → a(X, Y)→a(X|e,Z)•a(Z,Y)
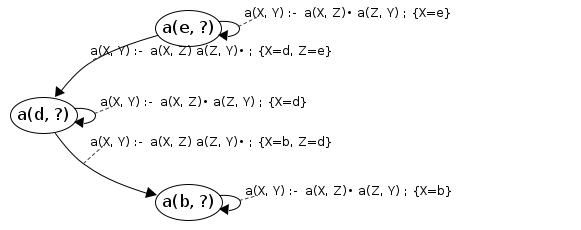	#7: JoinS: a(b, ?) → [b, e] will resume cont: Root("b", V0)→a("b",V0)• newVars: {V0=e} Processing Root() codePos Root("b", V0)→a("b",V0|e)• Reached end of rule, success! Root() → [b, e]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e] a(d, ?) → [d, e] a(b, ?) → [b, e] Root() → [b, e]✓
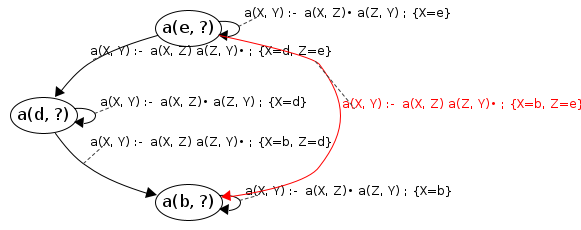	#8: JoinS: a(b, ?) → [b, e] will resume cont: a(X, Y)→a(X|b,Z)•a(Z,Y) newVars: {Z=e} Processing a(b, ?) codePos a(X, Y)→a(X|b,Z|e)•a(Z|e,Y) Calling: a(e, ?) [already processed]
p(b, ?) → [b, d] a(b, ?) → [b, d] Root() → [b, d]✓ p(d, ?) → [d, e] a(d, ?) → [d, e] a(b, ?) → [b, e] Root() → [b, e]✓
Iteration 5
Worklist - successes nJ Root() → (b, e) Worklist - continuations nJ a(e, ?) → a(X, Y)→a(X|b,Z|e), a(Z|e,Y)•
(No new calls or successes that can be further processed)
Iteration 6 [Fixed point reached]