Understanding the Takmela trace sheets

Do the traces look confusing? This guide will hopefully help you make sense of them, and help you further internalize the algorithm itself.

Summary:

• Takmela's algorithm runs in iterations, each composed of steps ; the trace is similarly divided into iterations
• A step is either the initial root call or a join
• Each step has its process tree (depicted on the right), and in this process tree each operation is either trivial (e.g matching terminals), a success, or calling a sub-rule
• Calling a subrule means adding a continuation, then processing what it can of the callee (in a subtree), then stopping
• The graph diagram represents the GSS (the K and newK tables), new continuations are shown in red
• The pane below the graph does the same for S and newS, the success/memoization table

Worklist labels summary

The running of a Takmela program (parsing or Datalog) happens in iterations, each of them composed of a series of steps.

K = {} ; newK = {} ; S = {} ; newS = {} ; awakenings = {}
callRootRule() 
while(true)
{
    kWorklist = diff(newK, K)
    sWorklist = diff(newS, S)
    
    if(kWorklist.size == 0 && sWorklist.size == 0) { break }     

    newK.clear() ; newS.clear()
    K = merge(kWorklist, K)
    S = merge(sWorklist, S)
    awakenings.clear()
    
    joinNewContinuationsWithPastSuccesses(kWorklist, S)
    joinNewSuccessesWithPastContinuations(sWorklist, K)
}

The 'zeroth' iteration happens before the while loop, and the only step therein is calling the root rule. Calling the root rule seeds the rest of the iterations since it can produce new successes (thus adding items to the sWorkList) or produce new calls and their continuations (adding items to kWorkList).

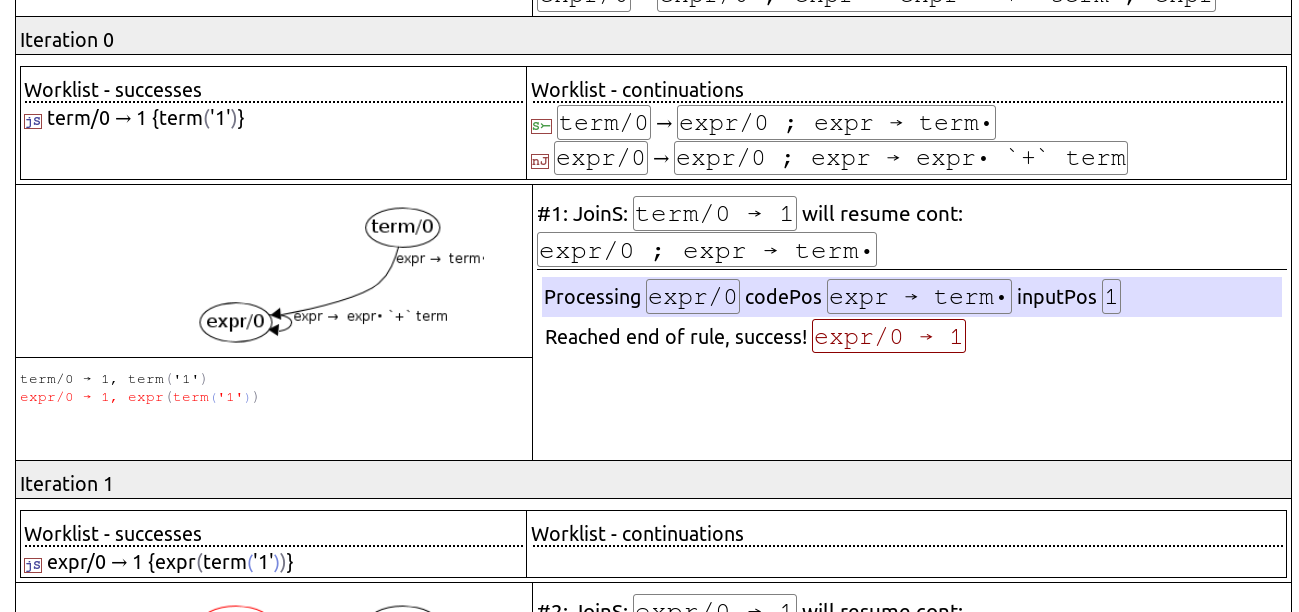
The first section shows the sWorklist and kWorklist, this is important since these worklists determine how the algorithm will go forward in the current iteration (and the algorithm will end when these worklists are empty).

Worklist items (new successes and continuations) move processing forward when they join with other items; a new success can join with a new or existing continuation, and a new continuation can do the same with successes.

The join criteria is the caller/callee relationship: if a new success represents the call a/5, and the K (continuations) table has an entry a/5 → (r/3 ; r → b a • c), then these two can join together to resume processing of the rule r from the specified code point. New continuations can make use of new/existing successes in the same way. The awakenings table is there to prevent the criss-cross problem where a new success and a new continuation join each other twice.

When a success joins a new or existing continuation, we call it a JoinS, and inversly when a new continuation joins a new or existing success, we call it a JoinK

The trace uses labels to show how worklist items join together, as explained below:

Processing trees

Inside each step, the algorithm processes a rule's contents. Suppose the algorithm was resuming a continuation such as (r/3 ; r → b a • '+' c d) : here's what would happen

1. Operations like matching the '+' are trivial; the algorithm will perform them and move to the next operation if the match succeeds (comparisons in Datalog are similarly handled).
2. If process found it has reached the end of a rule body (not depicted here!), it adds a new success and stops.
3. What happens when the algorithm encounters a call, like the call to c?
   1. It adds a new continuation to resume from, in our case it would be (r/3 ; r → b a '+' c • d)
   2. It invokes process on each of the callee's alternatives (unless the same call was already processed at this input position)
   3. It does not process any further elements in this rule body until the continuation is resumed

Interestingly, while the call to process is recursive, it doesn't have to be. This isn't the dynamic, unbounded recursion that needs a runtime stack; and a code generator could analyze the grammar and generate a specialized, non-recursive processRuleXyz(..) function for each of the grammar's nonterminals.